这是一个基本真实的故事。
一位在美国留学的阿拉伯学生阿卜杜拉Abdullah学成毕业了,阿卜计划回国找寻流失多年的祖上之宝-一颗硕大的南非钻石,它的曾祖父是一位富裕的石油商人,有感于子女们无所事事,不务正业,在他离世前将他的主要财产变卖购置了一颗未经加工的大钻石,藏秘于阿拉伯地区未知的神秘地方,只在家谱中留下一些线索。阿卜留学时有个好友一位中国留学生,离别时送他一个银立方盒并祝他此行好运。


阿卜根据家谱中留的线索,沿着被多年沉集风沙覆盖的阿拉伯古道徒步跋涉,风餐露宿,一路寻觅,历时三年的探宝苦行,终于在古道旁的一家古玩店的一堆石英、水晶石头中寻到,古店老板认定是水晶石,因此他以很低的价赎得,然后拿去以色列的钻石店家鉴定,确实是一枚价格不菲的南非钻石。
事情并未就此结束,阿卜的老父亲是一位传统的穆斯林教义信徒,共有八个子女,要求他将钻石分割八份,每个子女都均分一份,也就是说,阿卜自己只能得到八分之一分割后的钻石了。
阿卜思考了一天一夜,想到了一个钻石分割的办法,实际上是要求举行一场仪式,并且得到了老父亲的认可。
仪式的前段是根据穆斯林教义,父母与八位子女一同祷告,无时无刻跟随着真主的导引、彰显真主的大爱 …
仪式的第二阶段:
钻石交到老父亲手中,还有那个中国留学生送的银立方盒子,见照片,让老父亲将南非钻石藏于盒子的任一个节点后面,母亲做监察,关上盒子,将各节点编号。
仪式的第三段:
每个子女轮流进场,猜那个藏有钻石的节点号数,可以连续猜7次,直到猜中为止,猜中的可以分割得到钻石的七分之一,没有猜中的无权分割钻石。每当一个子女猜完后父母亲重新改变节点编号,这样前面的节点号就全改变了,避免作弊。阿卜无权猜节点,也就是说:如果子女们在7次猜的过程中都有一次猜中,阿卜就与钻石无缘了,他只能拿回那个中国留学生送的银立方盒作为纪念;如果有子女没猜中呢?剩下的归阿卜,他像是当庄家,也算是老父亲给他辛苦寻宝的一种回报。这个银立方盒子共有多少节点?120个节点,,您可数一数证实,有实物在。
最后结果怎样?大家可以用概率方法算一算,随机地猜7次也只有120分之7的概率 = 5.8%,这是个小功率,基本上是阿卜准赢,对不对?
而我为阿卜捏把汗,有一种猜法会让其他7个子女准赢,而阿卜挂零!
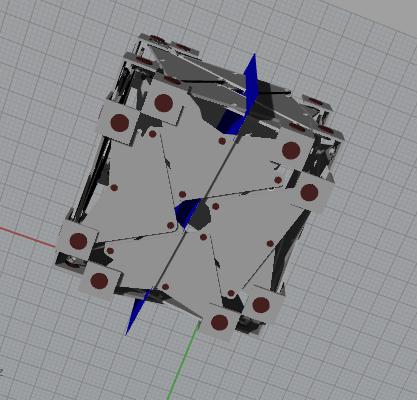
这种方法是:将银立方对中地分成两半,然后猜“钻石在左边的一半里,对吗”,如果回答“不是”,那就一定会在右边那一半,接着就对右边的一半再对分成两半,然后猜“在左边的一半,对吗”,如果回答“是”,接着就对左边的这一半再对分成两半,然后猜“在左边的一半,对吗”,如此猜7次,一定猜到那个藏钻石的节点!这个方法是二进制法(0 1),1为“是”,0为“不是”,一位二进制数是2,7位二进数是128, 这是每个高中生都学过的知识,银立方有120节点, 接近于7位二进制数128,所以猜7次一定找到藏钻石的节点!阿卜是毕业于名校的理工男,对二进制法想必是心知肚明,让每一个兄弟姐妹们猜7次,也许是给他们每人一个定赢的机会吧,可惜正如他们的曾祖父感叹的那样,许多子女都是无所事事惯了,现在只能与财富失之交臂。
好了,我们不谈钱啦,谈点高尚的。上面二进制的方法信息化大师香农Shannon定义为比特数,一个比特是一位二进制数,它是以2为底的对数, 如log8=3, log64=6, log128= 7, 香农在他的著名硕士论文《继电器与开关电路的符号分析》中把开关电路的“通”与“不通”和布尔代数的“真”与“假”对应起来,为比特(bit)的1和0。用比特这个概念来度量信息量,在上面银立方分割找钻石的例子中,寻宝的信息量是7。信息量的比特数和所有可能情况的对数函数 log 有关。

我在另一条微博上谈到银立方六个面的一个面节点如图,共有20个节点,如果将各个节点相连作为通道,以a0点为入口,以离人口最远的对角d2点为出口,实际上就是一个迷宫,每个节点都是一个道路岔口,有些像诸葛亮的八卦阵,盲目地走很难走出来。用香农的信息理论分析,20个节点的对数 log20接近于4,因此信息量是4,即最优的办法是经过4个节点就可以走出来。
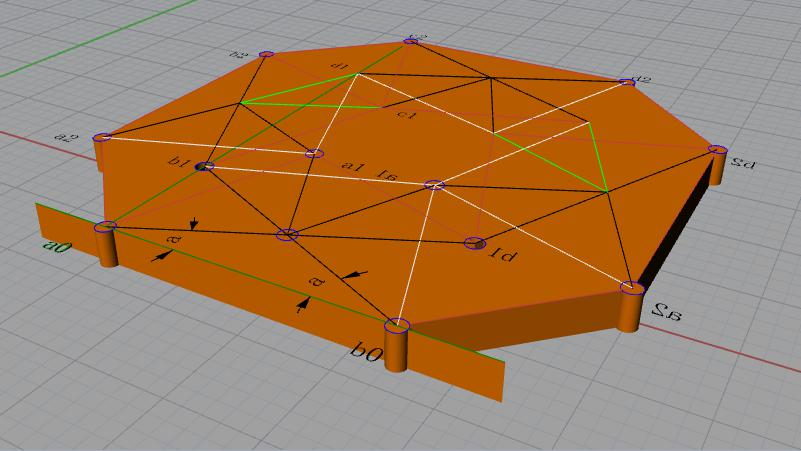
如果设比较近a0节点的a2节点为出口,走出迷宫的可能性更大,只需2个节点就走出来了


