如何将现实的问题转化为合适的数学模型,以一种新的思路解剖分析问题的本质。
2021.12.10

数学和语言学分属看起来毫不相干的两个学科,谷歌的科学家却以非常美的方式将它们联系起来,比如数学的余弦定理与新闻的分类,谷歌推出了自己的新闻服务,这些新闻不是记者写,也不是人工编辑的,而是由计算机整理、分类、和聚合各个新闻网的内容,自动生成的。
人工的新闻分类是由编辑先读懂新闻,找出主题内容,然后根据内容分类。但是计算机看不懂新闻,它只能“算”新闻而不是读新闻,这要求先把文字的新闻变成一组可计算的数字,然后再设计一个算法算出两篇新闻的相似度,进而从海量的新闻中找出相似度大的,以此完成新闻分类。
首先要在新闻中找数字,或者是“数字化”吧。新闻是传递信息的,而词是信息的载体,新闻的信息和词的语义是联系在一起的,用单文本词汇频率/逆文本频率值TF-IDF来衡量,如果和新闻主题有关的那些实词频率高,TF-IDF值很大。
例如:
单词编号 汉字词 TF-IDF 值
-------------------------------------------
1 阿 0
2 啊 0.0034
3 阿斗 0
4 阿姨 0.00052
... ...... ....
789 服装 0.034
... .... ....
6400 做作 0.075
如果单词表中的某个词在新闻中没有出现,对应的值为零,那么这64000个数,组成了一个64000维的向量。我们就用这个向量来代表这篇新闻,称之为新闻的特征向量。每一篇新闻都可以对应这样的一个特征向量,向量中每一个维度的大小代表每个词对新闻主题的贡献。
学过向量代数的朋友都知道,向量实际上是多维空间中从原点出发的有向线段。
不同的新闻,因为文本长度的不同,它们的特征向量各个维度的数值也不同。一篇10000字的文本,各个维度的数值都比一篇500字的文本来得大,因此单纯比较各个维度的大小并没有态度意义。但是,向量的方向却有很大的意义。如果两个向量的方向一致,说明相应的新闻用词的比例基本一致。因此可以通过计算两个向量的夹角来判断对应的新闻主题的接近程度。而计算两个向量的夹角,用余弦定理就可以了。它描述了三角形中任何一个夹角和三个边的关系,换句话说,给定三角形的三条边,可以用余弦定理求出三角形各个角的角度。
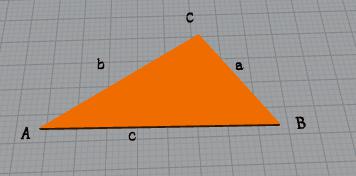
COS A = (b^2 + c^2 - a^2 ) / 2bc
等价的向量公式:
COS A = <a, c >/ (|b|.|c|)
其中,分母表示两个向量b 和 c 的长度,分子表示两个向量的内积。举个新闻具体的例子,假如新闻X和新闻Y对应的向量分别是
x1, x2, ..., x6400 和 y1,y2, ..., y6400,
那么它们夹角的余弦等于
COS θ = ( x1y1 + x2y2 + ... + x6400y6400)/(x1^2 + x2^2 + ... + x6400^2 )^1/2 . (y1^2 +y2^2 + ... + y6400^2)^1/2
(因为打印关系说明一下:x1^2 为 x1的平方,如此类推)
由于向量中的每一个变量都是正数,因此余弦的取值在0 和 1 之间,也就是说夹角在0度和90度之间,当两条新闻向量夹角的余弦等于 1 时,这两个向量的夹角为零,即两条新闻完全相同,当两个向量的夹角接近于零时,两条新闻相似,可以归为一类;夹角越大,两条新闻越不相关,当夹角为正相交即90度时,说明两篇新闻根本没有相同的主题词,它们毫不相关。计算机只要不到一秒的时间就得出来结果,在计算中的技巧方式和方法的应用这里不展开了;一个人工编辑读完一篇新闻文本得数分钟哦,计算机工作速度比编辑人员快一百倍。
这样的数学模型很准(数字量化了),很快,很美!不是吗?
下面我们换个话题,拿机器人本体说说事,串联机器人和并联机器人都是杆端相连的,所以它们的连接节点都比较少,例如串联只有3个节点(两段臂串联),并联有6个(三杆并联)或8个(四杆并联),但如果进入到机器人第三种本体形式--面域联,其节点数猛然增加,例如类正方体的面域联有120个固定节点,加上多个非固定节点,非固定节点是在面域区块上安装机械臂或传感器等装备的节点,类球体的面域联有60个固定节点,加上多个非固定节点的节点。节点的有序有机地分散连接使得机器人的受力趋于合理优化,绕过了精密减速机这个关键零部件,使得机器人的成本大幅降低。显然,我们已经进入了一个新的技术层面,如何提前规划?

首先是数字化,像前面的新闻分类的例子那样,建立了数字化的模型,然后优选算法,例如上面使用的余弦定理,利用计算机这个强大的资源,大面积地收割产品庄稼。
下图是类正方体的6个平面之一的节点图

读者可能发现,图中的多节点连接应用了计算机理论中的“树”结构。其算法可以采用数学的向量和矩阵,这样便于电脑的计算和优化。
首先选取坐标系,这里选择直角坐标系,a0为原点坐标,通过解析每个节点的算式和方法得出每个节点的向量值。
例如:
b1点的三维向量是 [ 0,lsin(a), 0 ]
b2点的三维向量是 [-lsin(a),lsin(a)+lcos(a),0]
... ...
b120点的三维向量是 [lcos(a), 2l(sin(a) +lcos(a)), 2l(sin(a) + cos(a)) ]
其中: l-- 面域区块斜边长,
a-- 转动变量。
转动变量a是几何变量,输入a 的值后各节点的空间位置即可唯一地确定。
同理,我们得到类立方体其它5个面域区块的节点向量,共120个节点向量。这些向量元素可以组成一个大的120 x 3 的矩阵,在这个矩阵中,每一行对应类立方体的一个节点,每一列对应各个节点的一个维度的值,这样数字化以后,计算机可以方便的提取数据和快速运算。
0 lsin(a) 0
A = ( -lsin(a) lsin(a)+lcos(a) 0 ) (1.1)
... ... ...
lcos (a) 2l(sin(a) + cos(a)) 2l(sin(a) + cos(a))
如果如下图示这样立起来,只需将坐标系旋转转换成新的坐标系即可。

在节点上或面域区块上任何地方(称为非固定节点)可以安装多个多轴的机器人,如下图所示在类立方体上安装了3个六轴的机器人,这三个机器人的终端坐标任何定呢?只需将类立方体的节点向量或非固定节点向量与机器人的终端向量相加就可以了。

机器人的终端向量是多个轴电机旋转变量的函数,如6个电机的旋转变量为a1,a2,…,a6, 该机器人的终端向量为
( X(a1,a2,…,a6), Y(a1,a2,…,a6),Z(a1,a2,…,a6) );
该函数参量各生产厂家都是现有的,因为要实现机器人产品的终端控制,机器人产品必须有这样的函数参量。而类立方体的节点向量已经在上式(1.1)的矩阵给出了,如果安装在非固定节点,可以用相邻两个节点向量的减和数乘的方法得到非固定节点的向量。
这样我们得到三个机器人与类立方体分联的所有终端向量,该例子中有三个。
它们分别是:
设 ( x1, y1, z1 ) 为安装节点1的向量,( X1(a1,a2,…,a6), Y1(a1,a2,…,a6), Z1(a1,a2,…,a6) )为机器人1的向量;
( x2, y2, z3 ) 为安装节点2的向量,( X2(a1,a2,…,a6), Y2(a1,a2,…,a6), Z2(a1,a2,…,a6) )为机器人2的向量;
( x3, y3, z3 ) 为安装节点3的向量,( X3(a1,a2,…,a6), Y3(a1,a2,…,a6), Z3(a1,a2,…,a6) )为机器人3 的向量;
( x1+ X1(a1,a2,…,a6), y1+ Y1(a1,a2,…,a6), z1+ Z1 (a1,a2,…,a6) );
( x2 + X2(a1,a2,…,a6), y1+ Y2(a1,a2,…,a6), z1+ Z2(a1,a2,…,a6) );
( x3 + X3(a1,a2,…,a6), y1+ Y3(a1,a2,…,a6), z1+ Z3(a1,a2,…,a6) );
这三个终端向量组成了一个 3 x 3 的矩阵,它是类立方体与3个机器人分联的结果。3个机器人是联控的,并且同时做不同的三个工作。
x1+ X1(a1,a2,…,a6), y1+ Y1(a1,a2,…,a6), z1+ Z1 (a1,a2,…,a6)
B = ( x2 + X2(a1,a2,…,a6), y1+ Y2(a1,a2,…,a6), z1+ Z2(a1,a2,…,a6) ) (1.2)
x3 + X3(a1,a2,…,a6), y1+ Y3(a1,a2,…,a6), z1+ Z3(a1,a2,…,a6)
同理,我们可以得到类立方体与n个机器人分联的矩阵,它有n 个终端向量,同时做不同的n 个工作。这n个终端向量组成了一个 n x 3 的矩阵,
x1+ X1(a1,a2,…,a6), y1+ Y1(a1,a2,…,a6), z1+ Z1 (a1,a2,…,a6)
C = ( x2 + X2(a1,a2,…,a6), y1+ Y2(a1,a2,…,a6), z1+ Z2(a1,a2,…,a6) ) (1.3)
… …
xn + Xn(a1,a2,…,a6), yn+ Yn(a1,a2,…,a6), zn+ Zn(a1,a2,…,a6)
以上只是类立方体的三维特征向量矩阵,这是远不够的,因为面域联机器人在技术上有许多改进,技术特征还有许多信息需一并储存,如1.节点轴承有相对金属轴承更加优良的特殊材料轴承,如聚四氟乙烯轴承、乙缩醛轴承、尼龙轴承等,它们的性价比好于金属轴承;2,面域区块已经不同于传统的杆状臂,它们有许多新颖的结构如筋骨结构,几何外形增补结构等;3.面域机器人大量的采用各种传感器,如力觉、触觉、视觉、位置、速度、化学传感器等;4. 面域联形式还有许多种类,诸如类球形、金字塔形、类长方矩形、弧形臂等;5. 面域联的混联后衍生出更多的结构形式,例如类球于类立方体混联,多边金字塔形于类立方体混联,面域联于串联、并联形成的混联等;6. 许多物理特征需要数字化的表述,如材料、硬度等;6.机器人工作环境是化工、电子、食品、医疗、有污染吗?7. 是在水下、室内或野外、还是空间站等等,都需要逐项编码,使得计算机可以方便的提取、运算和结果输出,便于系统采用计算机的操作应用机器人产品。这个目标无非是用更大一些的矩阵包括容纳这些逐项的编码,并且将串联和并联机器人及其它形式也容纳进去, 这就是我们提议的机器人特征向量矩阵( M x N).,我们在《机器人特征向量分类》一文中会比较详细地阐述。
总之,定义一个这样的M x N 的 机器人特征向量 A:

机器人特征向量可以是机器人行业的数字化标准,该数字化标准可以有效地帮助生产线的规划集成、组装、工艺规划,在线控制,维护修理等,它是智能化的基础,建立这样的机器人数字化的标准很有必要。具体定义和数字编码当然应由国际机器人协会牵头组织实现标准化和推广,我们麻麻垫,这里只是是抛砖引玉哈。
国际范围内海量的机器人的生产和在各行业的应用是一个不可逆转的大趋势,十年内可以达十亿台套的量,通常可以达到当前手机的数量和价位, 2008年的金融危机刺激了机器人的推广,由于经济的突然崩溃迫使许多公司裁员,那些难以招到员工的企业也开始求助于机器人来填补空缺职位,自动化使得业务保持正常运行,并且长期看成本要低很多。经济浩劫后,更多公司会选择机器人的投入,因为机器人带来许多红利。现在的COVID-19疫情比之2008年的金融危机带来的经济动荡更加严重,机器人的品种和数量必定激增。机器人的标准化、智能化、信息化管理迫在眉梢,机器人数字化标准是这个千亿产业迈开的关键一步。

